Attention: This article describes an approach to solve Project Euler problem 345, if you want to solve it by yourself, do not read on.

Recreational Operational Research

The Max-Flow and the closely related Min-Cost Flow problems are very interesting and provide a lot of possible application areas. Many problems can be modeled as an instance and solved efficiently. In fact, Max-Flow is P-complete, i.e, any problem in P can be reduced to it in polynomial time.

Problem Description

The Project Euler problem 345 looks for a choice of elements from a matrix in such a way that for each row and column exactly one element is chosen, and that the sum of the elements is maximized. A simple example:

1	4
1	10

Here, only two choices are possible, either {1, 10} or {1, 4}. It is obvious, that chosing {1, 10} maximizes the result with the optimal value of 11.

Like many Project Euler exercises, the straight-forward approach is to try all combinations. While this is feasible for small examples, the larger (but still at most medium-sized), real problem uses a 15x15 matrix, resulting in 15! (1307674368000) possibilities, way too much for trial and error.

Solving the Problem using Network Flow

One efficent, and in my opinion, very elegant approach to solve the problem is to express it as a Min Cost Flow instance. This can be done as follows:

• to ensure that only one element per row is selected, each entry of the matrix is transformed into two nodes, a left and a right one, connected via an arc with capacity 1
• each left node is also connected via an arc with capacity 1 with the left node of the next column
• the selection of an element is modeled as flow form a left node to a right node
• an element is not selected if there is a flow from its corresponding left node to the next left one
• all nodes of the first column are connected to the source with arcs with capacity 1, to ensure only 1 flow unit per row
• to ensure the selection of exactly one element per column, each right node of a column is connected via an arc of capacity 1 to an additional column node
• each column node is connected to the sink via an arc with capacity 1

The resulting network has a size (nodes and edges) linear in the number of matrix entries of the original problems. For the example this looks as follows:

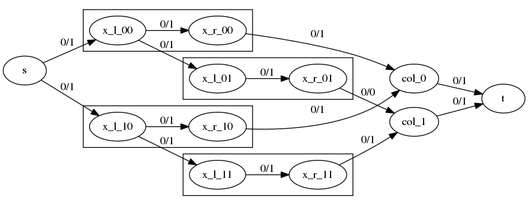
Here, x_l_ij represents the left node of the matrix entry (i, j), x_r_ij the right node, col_k the column node for column k, s the source, t the sink and the labels represent flow/capacity of the arc.

When we compute a maximal flow for this network, one possibility for a flow of value 2 looks as follows:

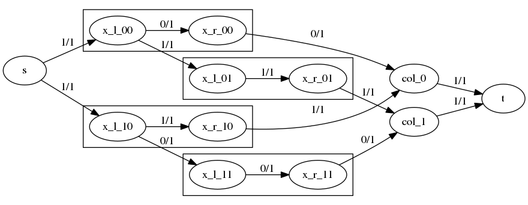
This solution corresponds to selecting the matrix elements (0, 1) and (1, 0), i.e., the non-optimal solution. In order to get the desired solution, we add the cost to the edges, they consist now of flow/capacity/cost. As the algorithm minimizes the cost, but we want to maximize our objective function, we use the negative costs; minimization of a scalar function is equivalent to maximization of its negation.

The minimal cost flow for the network looks like this:

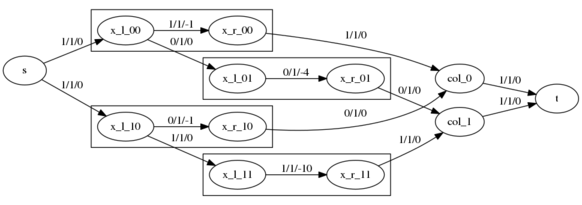
This is a flow of value 2 with cost -11, as we send one flow unit over the arc from x_l_00 to x_r_00 with cost -1 and one flow unit from x_l_11 to x_r_11 with cost -10; this being exactly the solution we are looking for.

The same technique can be used to solve the problem instance given in the Project Euler Description. While it is tempting to implement own algorithms for Max-Flow and Min-Cost Flow, it is much simpler to use s.th. existing, e.g., the Google OR-tools which provide bindings for Python. With a few lines of Python and one call to the solver, the solution is calculated basically instantly.

Alternatives

There are of course alternative solutions for this problem. One such approach is the Hungarian Method which also is polynomial. The problem can be modeled in different ways as Integer Linear Program, very generally as a Constraint Satisfaction Problem with an objective function or even using a Dynamic Programming approach.